91 As A Fraction: Steps And Explanation
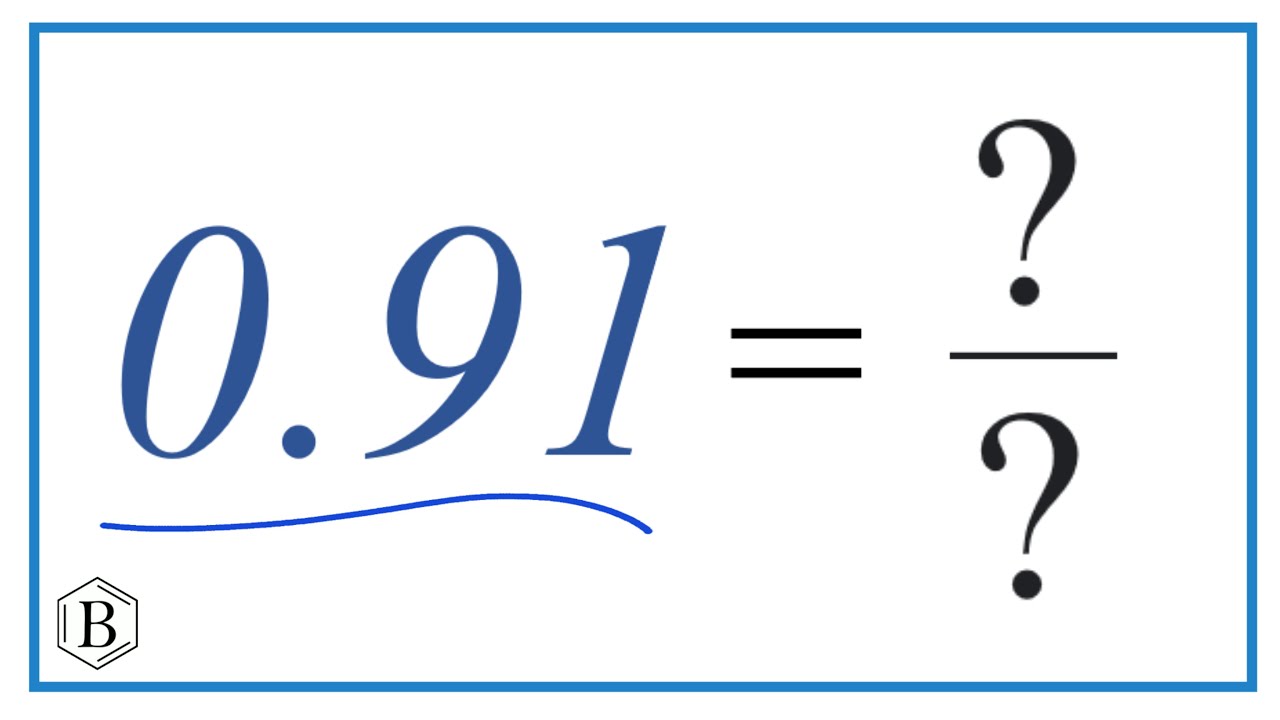
91 As A Fraction: Steps And Explanation. Discover more detailed and exciting information on our website. Click the link below to start your adventure: Visit Best Website. Don't miss out!
Table of Contents
91 as a Fraction: A Simple Guide with Steps and Explanation
Converting decimals to fractions might seem daunting, but it's a fundamental skill in mathematics with applications across various fields, from baking to engineering. Today, we'll tackle a specific example: expressing 91 as a fraction. This seemingly simple task offers an excellent opportunity to understand the underlying principles of decimal-to-fraction conversion. This guide provides a step-by-step explanation, ensuring even beginners can master this concept.
Understanding the Basics: Decimals and Fractions
Before diving into the conversion of 91, let's refresh our understanding of decimals and fractions. A decimal is a number expressed in the base-ten numeral system, using a decimal point to separate the integer part from the fractional part. A fraction, on the other hand, represents a part of a whole, expressed as a ratio of two integers – the numerator (top number) and the denominator (bottom number).
Converting 91 to a Fraction: A Step-by-Step Approach
Since 91 is a whole number, it doesn't have a fractional part in its decimal representation. Therefore, the conversion is remarkably straightforward. To express 91 as a fraction, we simply place 91 over 1:
- Step 1: Write the whole number as the numerator. In this case, the numerator is 91.
- Step 2: Write 1 as the denominator. This represents the whole.
- Step 3: The resulting fraction is 91/1.
Therefore, 91 as a fraction is 91/1.
Why is 91/1 the Correct Fraction?
The denominator of a fraction indicates how many equal parts the whole is divided into. A denominator of 1 signifies that the whole is not divided at all; it remains a single, undivided unit. The numerator then represents how many of these undivided units we have—in this instance, 91. This clearly illustrates that 91/1 accurately represents the whole number 91.
Equivalent Fractions of 91
While 91/1 is the simplest and most accurate representation of 91 as a fraction, it's crucial to remember that there exist infinitely many equivalent fractions. For instance, multiplying both the numerator and denominator by the same number will result in an equivalent fraction. Examples include:
- 182/2
- 273/3
- 364/4
However, 91/1 remains the simplest form as it uses the smallest possible whole numbers.
Applications and Further Learning
Understanding decimal-to-fraction conversion is essential for various mathematical operations and real-world applications. From calculating proportions in recipes to solving complex algebraic equations, mastering this fundamental skill opens doors to more advanced mathematical concepts.
Want to further your understanding of fraction manipulation? Explore resources on:
- Simplifying fractions: Learn how to reduce fractions to their simplest form.
- Adding and subtracting fractions: Master the techniques for combining fractions.
- Multiplying and dividing fractions: Understand the rules for these operations.
By understanding the basic principles outlined in this article, you can confidently convert whole numbers like 91 into their fractional equivalents. Remember, practice makes perfect! Try converting other whole numbers into fractions to solidify your understanding.
Thank you for visiting our website wich cover about 91 As A Fraction: Steps And Explanation. We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and dont miss to bookmark.
Featured Posts
-
 Fantastic Four First Steps Trailer Unveils Comic Accurate Costumes
Feb 05, 2025
Fantastic Four First Steps Trailer Unveils Comic Accurate Costumes
Feb 05, 2025 -
 Cricket World Divided Khawajas Support For Axed Journalist
Feb 05, 2025
Cricket World Divided Khawajas Support For Axed Journalist
Feb 05, 2025 -
 Beyond The Jab Exploring Weight Loss Options For Injection Intolerant Individuals
Feb 05, 2025
Beyond The Jab Exploring Weight Loss Options For Injection Intolerant Individuals
Feb 05, 2025 -
 Current Time In Boston Time Zone And Daylight Saving
Feb 05, 2025
Current Time In Boston Time Zone And Daylight Saving
Feb 05, 2025 -
 Juliette Binoche Presidente Du Jury Cannes 2025
Feb 05, 2025
Juliette Binoche Presidente Du Jury Cannes 2025
Feb 05, 2025
Latest Posts
-
 Osint Defender Twitters New Privacy Shield
Feb 05, 2025
Osint Defender Twitters New Privacy Shield
Feb 05, 2025 -
 Tributes Pour In Following Death Of Brian Murphy George And Mildred Star
Feb 05, 2025
Tributes Pour In Following Death Of Brian Murphy George And Mildred Star
Feb 05, 2025 -
 Onhockey Tv Stream Hockey Games Live And On Demand
Feb 05, 2025
Onhockey Tv Stream Hockey Games Live And On Demand
Feb 05, 2025 -
 Sam Kerr Trial Officers Omission Of Stupid And White Impact Questioned
Feb 05, 2025
Sam Kerr Trial Officers Omission Of Stupid And White Impact Questioned
Feb 05, 2025 -
 System Verilog Assertions Mastering Verification Without Dist
Feb 05, 2025
System Verilog Assertions Mastering Verification Without Dist
Feb 05, 2025
