Understanding Decimal To Fraction Conversion: The Case Of 0.91
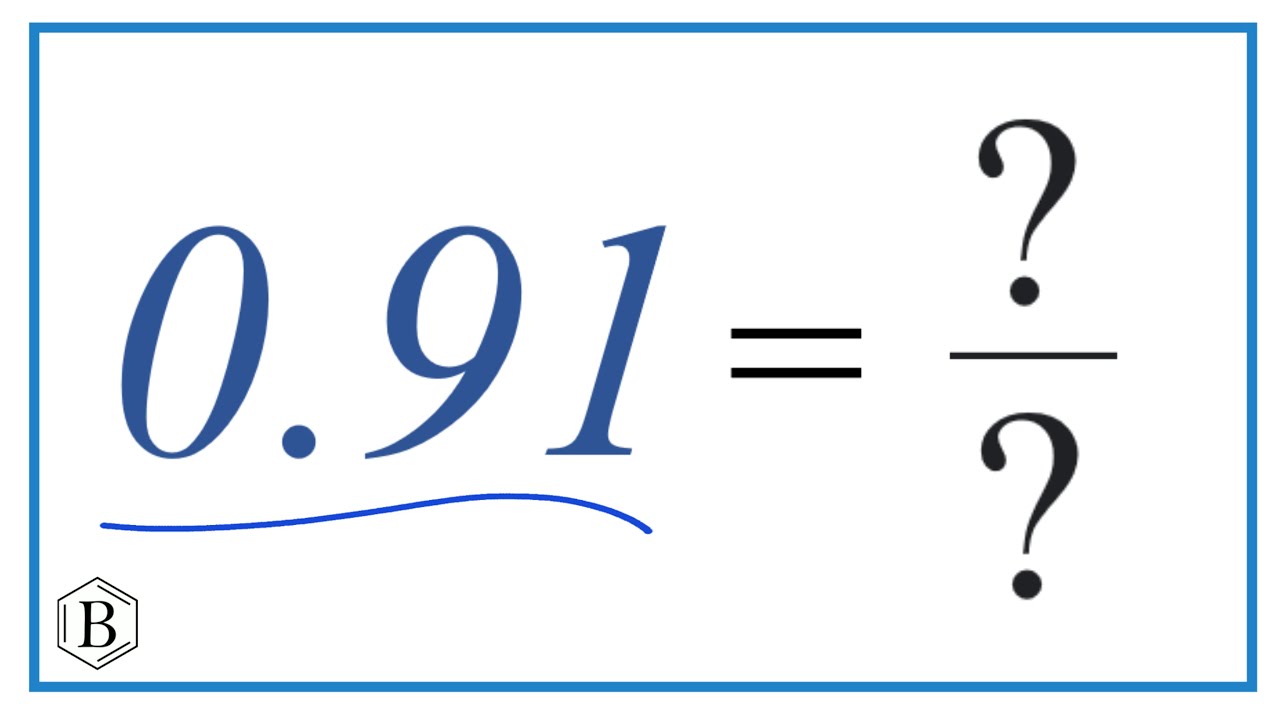
Understanding Decimal To Fraction Conversion: The Case Of 0.91. Discover more detailed and exciting information on our website. Click the link below to start your adventure: Visit Best Website. Don't miss out!
Table of Contents
Understanding Decimal to Fraction Conversion: Decoding 0.91
Decimals and fractions are two sides of the same coin – both represent parts of a whole. Mastering the conversion between them is crucial for success in math, from elementary school arithmetic to advanced scientific calculations. Today, we'll delve into the process, using the decimal 0.91 as our example, and equip you with the knowledge to tackle any decimal-to-fraction conversion with confidence.
Why is Decimal to Fraction Conversion Important?
Understanding decimal to fraction conversion is more than just a classroom exercise. It's a fundamental skill applicable in various real-world scenarios:
- Baking and Cooking: Recipes often require precise measurements, and converting decimals to fractions ensures accuracy.
- Engineering and Construction: Precise calculations are essential, and fractions offer a more intuitive understanding of proportions in certain contexts.
- Financial Calculations: Dealing with percentages and proportions requires a strong understanding of both decimals and fractions.
Converting 0.91 to a Fraction: A Step-by-Step Guide
The process involves a few simple steps:
-
Write the decimal as a fraction with a denominator of 1: 0.91 can be written as 0.91/1.
-
Multiply the numerator and denominator by a power of 10 to remove the decimal: Since there are two digits after the decimal point, we multiply both the numerator and denominator by 100: (0.91 x 100) / (1 x 100) = 91/100.
-
Simplify the fraction (if possible): In this case, 91 and 100 share no common factors other than 1, meaning the fraction is already in its simplest form.
Therefore, 0.91 as a fraction is 91/100.
Beyond 0.91: Tackling More Complex Decimal Conversions
While 0.91 provided a straightforward example, other decimals might require additional steps. For instance:
- Repeating Decimals: Converting repeating decimals (like 0.333...) requires a different approach involving algebraic manipulation. We'll cover this in a future article – stay tuned!
- Decimals with Multiple Digits: The same principle applies to decimals with more digits after the decimal point; simply multiply by the appropriate power of 10. For example, 0.1234 would become 1234/10000.
Mastering Fraction to Decimal Conversion: The Reverse Process
It's also important to be comfortable converting fractions to decimals. This is often done by simply dividing the numerator by the denominator. For example, 3/4 is calculated as 3 ÷ 4 = 0.75. Understanding both conversions provides a comprehensive understanding of numerical representation.
Conclusion: Unlocking the Power of Numerical Fluency
Proficiency in converting between decimals and fractions is a cornerstone of mathematical understanding. By grasping the simple steps outlined above, you'll unlock a greater ability to navigate numerical challenges across various fields. Practice regularly and remember that mastering these conversions will enhance your problem-solving skills significantly. Do you have any tricky decimal-to-fraction conversions you'd like to share? Let us know in the comments below!
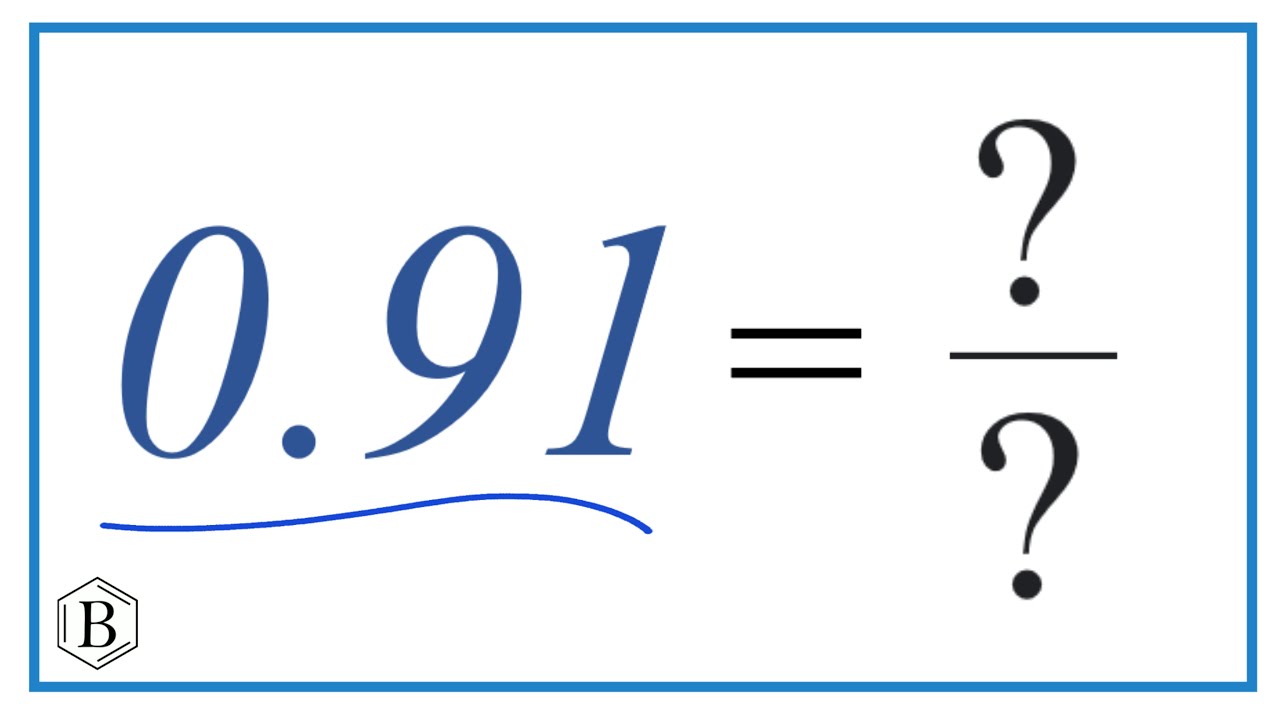
Thank you for visiting our website wich cover about Understanding Decimal To Fraction Conversion: The Case Of 0.91. We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and dont miss to bookmark.
Featured Posts
-
 Expanded Rapid Cancer Testing A World Cancer Day Success Story
Feb 05, 2025
Expanded Rapid Cancer Testing A World Cancer Day Success Story
Feb 05, 2025 -
 The Untold Earnhardt Story Family Feuds And Racing Rivalries
Feb 05, 2025
The Untold Earnhardt Story Family Feuds And Racing Rivalries
Feb 05, 2025 -
 The Current Time In Jamaica A Quick Time Check
Feb 05, 2025
The Current Time In Jamaica A Quick Time Check
Feb 05, 2025 -
 C Batteries Your Ultimate Buying Guide For Long Lasting Power
Feb 05, 2025
C Batteries Your Ultimate Buying Guide For Long Lasting Power
Feb 05, 2025 -
 Connecting Globally Tis Churchofjesuschrist Org Community Features
Feb 05, 2025
Connecting Globally Tis Churchofjesuschrist Org Community Features
Feb 05, 2025
