Understanding Radical Form In Calculus
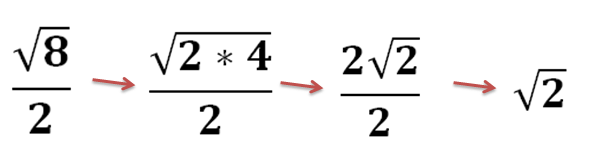
Understanding Radical Form In Calculus. Discover more detailed and exciting information on our website. Click the link below to start your adventure: Visit Best Website. Don't miss out!
Table of Contents
Decoding the Enigma: A Comprehensive Guide to Understanding Radical Form in Calculus
Calculus, a cornerstone of higher mathematics, often presents students with seemingly insurmountable challenges. One such hurdle is mastering the manipulation and simplification of expressions involving radical forms. Understanding radical form in calculus is not merely about simplifying equations; it's about gaining a deeper understanding of fundamental concepts and efficiently solving complex problems. This article provides a comprehensive guide to navigating the complexities of radical forms within the realm of calculus.
What is Radical Form in Calculus?
In the context of calculus, radical form refers to the representation of mathematical expressions using roots (square roots, cube roots, and higher-order roots). These expressions often appear in differentiation, integration, and limit problems. Understanding how to simplify and manipulate these radical expressions is crucial for achieving accurate and efficient solutions. For example, expressions like √x, ³√(x²+1), or (x⁴ + 2x)¹ᐟ³ are all examples of radical forms commonly encountered in calculus.
Key Techniques for Simplifying Radical Forms
Several techniques are essential for simplifying radical expressions in calculus. Mastering these will significantly improve your problem-solving capabilities:
-
Rationalizing the Denominator: This involves eliminating radicals from the denominator of a fraction. This is particularly important when dealing with limits and derivatives, as it can simplify calculations and avoid indeterminate forms. For example, simplifying 1/√x to √x/x makes further manipulations easier.
-
Using the Properties of Exponents: Radical expressions can be rewritten using fractional exponents. This equivalence is fundamental to calculus, allowing for the application of power rules in differentiation and integration. Remember that √x = x¹ᐟ², ³√x = x¹ᐟ³, and so on.
-
Factoring and Simplifying: Before applying calculus techniques, always simplify the expression as much as possible. Factoring out common terms and simplifying radicals can greatly reduce the complexity of the problem.
-
Conjugate Multiplication: When dealing with expressions containing sums or differences of radicals, multiplying by the conjugate can be highly effective in simplifying the expression. This technique is frequently used to rationalize denominators involving sums or differences of square roots.
Radical Forms in Differentiation and Integration
Radical forms frequently appear in differentiation and integration problems. Understanding how to manipulate these forms is crucial for finding derivatives and integrals accurately.
Differentiation: When differentiating expressions involving radicals, it's often advantageous to rewrite them using fractional exponents before applying the power rule. For example, differentiating √x (which is x¹ᐟ²) becomes straightforward using the power rule: d/dx(x¹ᐟ²) = (1/2)x⁻¹ᐟ².
Integration: Similarly, integrating expressions containing radicals often requires rewriting them using fractional exponents and applying the power rule for integration. More complex integrals may require techniques like u-substitution or integration by parts, but simplification through manipulation of radical form is always the first step.
Advanced Applications and Problem Solving
Understanding radical forms extends beyond basic simplification. Mastering this concept is vital for tackling more advanced topics in calculus, including:
- Implicit Differentiation: Finding derivatives of implicitly defined functions often involves manipulating radical expressions.
- Related Rates Problems: These problems frequently incorporate expressions involving radicals, requiring skillful manipulation for solving.
- Optimization Problems: Finding maximum or minimum values frequently necessitates working with radical expressions.
Conclusion: Mastering the Fundamentals
Proficiency in simplifying and manipulating radical forms is a cornerstone of success in calculus. By mastering the techniques outlined above and consistently practicing, students can confidently tackle even the most challenging problems involving radical expressions. Regular practice and a clear understanding of the fundamental properties of exponents and radicals are key to unlocking a deeper understanding of calculus. Remember to always simplify before differentiating or integrating for efficient and accurate solutions. Start practicing today and watch your calculus skills soar!
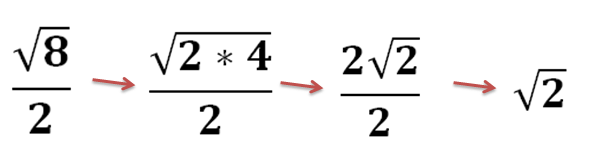
Thank you for visiting our website wich cover about Understanding Radical Form In Calculus. We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and dont miss to bookmark.
Featured Posts
-
 Managing Olanzapine Weight Gain Strategies And Support
Feb 05, 2025
Managing Olanzapine Weight Gain Strategies And Support
Feb 05, 2025 -
 Kingdom Come Deliverance 2 Improved Gameplay Mechanics
Feb 05, 2025
Kingdom Come Deliverance 2 Improved Gameplay Mechanics
Feb 05, 2025 -
 Jalen Brunson Height Revealed Shoeless Measurement And Nba Comparisons
Feb 05, 2025
Jalen Brunson Height Revealed Shoeless Measurement And Nba Comparisons
Feb 05, 2025 -
 Understanding Bostons Time Zone A Complete Guide
Feb 05, 2025
Understanding Bostons Time Zone A Complete Guide
Feb 05, 2025 -
 Schweden Schuesse An Schule Aktuelle Lage Und Opfer
Feb 05, 2025
Schweden Schuesse An Schule Aktuelle Lage Und Opfer
Feb 05, 2025
